Speeding up Single Cell
Tumor Mutation Tree Inference

Deep Dive into Computational Statistic in Cancer Genomics

Feb 2023 - Oct 2023

For my 2nd Master thesis at ETH Zürich in Biotechnology, I wanted to learn more about computational/bayesian statistics applied in genomics.

Brief

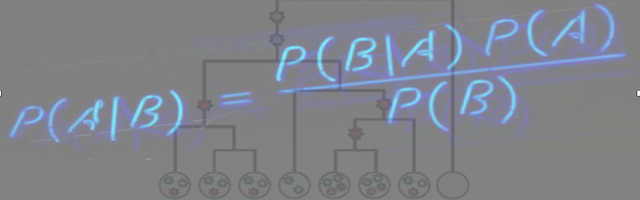
Cancer progression is an evolutionary process in which cells with different characteristics compete with each other. Understanding the cell heterogeneity is important for prognosis and suggesting the right treatment. Single-cell DNA sequencing allows one to measure mutations in selected cells at a specific time point. The tumor phylogeny problem aims at reconstruction of the whole evolutionary history of the tumor based on this single snapshot, in the form of a mutation tree.

Although there exist principled methods, such as SCITE [1], which traverse the space of all possible mutation histories to suggest the most likely ones, they can be too slow and computationally intense to run. Hence, there is a sparking interest in fast heuristic methods, which can be used to approximate a single most-likely tree.

[1] Tree inference for single-cell data, Genom Biology, Jahn et al. 2016

Why this?

Learn advanced computational statistics.

Working on single-cell genomic data sounds cool.

Throw in some high-performacne computing.

Escaping the burden of feeding your cells in the wet-lab.

Formal Abstract

Understanding the mutational intra-tumour heterogeneity within tumours is crucial to developing effective personalised cancer therapies. Bayesian Markov chain Monte Carlo (MCMC) sampling schemes have proven successful and trusted in reconstructing tumour progression histories, particularly mutation trees. To understand the effectiveness of mutation tree MCMC methods and their required runtimes, it is crucial to understand how quickly the empirical distribution of the MCMC converges to the posterior distribution.

We quantify the MCMC exploration of the mutation tree space for the landmark inference scheme SCITE using tree similarity measures. In this simulation study, the tree similarities map features informative of a tumour’s clonal expansion from the mutation tree space to a scalar space, allowing the study of the MCMC exploration. Quantification of the exploration is provided by the novel application of convergence diagnostics established in continuous space to the discrete space of mutation trees via tree similarities.

Consequently, we estimate the required runtime of SCITE for simulated data, which may imply significantly reduced runtimes for real-world datasets.

Further, we find the dependence of the initial state of the MCMC to vanish quickly. We recommend trialling the significant reduction of the warm-up period for real-world datasets, implying another reduction in required runtime. In the process of exploring initialisation strategies, we validated the performance of the fast heuristic inference method HUNTRESS.

Lastly, we investigate the topology of the Bayesian tree posterior, which is thought to contain multi-modalities potentially. For simulated data, we did not find evidence for any multi-modalities justifying the design of SCITE as a single-chain MCMC scheme.